空间向量是数学中的重要概念，具有广泛的应用价值，为了更好地理解和掌握空间向量的相关知识，专题练习是必不可少的，本文将围绕空间向量的基本概念、性质、运算以及实际应用等方面，设计一系列专题练习，帮助读者深化理解，提高实战应用能力。

空间向量的基本概念与性质

1、空间向量的定义：在三维空间中，既有大小又有方向的量称为向量。

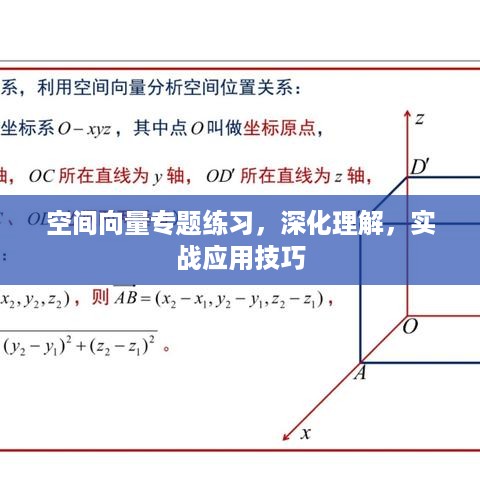
2、向量的表示：可以通过坐标来表示向量，如a = (x, y, z)。

3、向量的性质：包括加法、数乘、数量积、向量积等性质。

空间向量的运算

1、向量的加法与数乘：向量的加法遵循平行四边形法则和三角形法则，数乘则是指用实数与向量相乘。

2、向量的数量积：数量积表示两个向量的夹角和模长，用于判断两向量的垂直关系。

3、向量的向量积：向量积表示两个向量叉乘的结果，其结果为一个新的向量，其方向垂直于原两个向量构成的平面。

专题练习

专题一：向量的基本概念与表示

1、简述向量的定义。

2、给出向量的坐标表示方法。

专题二：向量的性质与运算

1、简述向量的加法、数乘、数量积和向量积的性质。

2、通过实例练习向量的加法和数乘运算。

3、掌握数量积和向量积的运算方法，并判断向量的垂直关系。

专题三：空间向量应用

1、力的合成与分解：通过向量的加法与数乘，理解力的合成与分解原理。

2、平面几何问题：利用向量解决平面几何中的距离、角度和面积等问题。

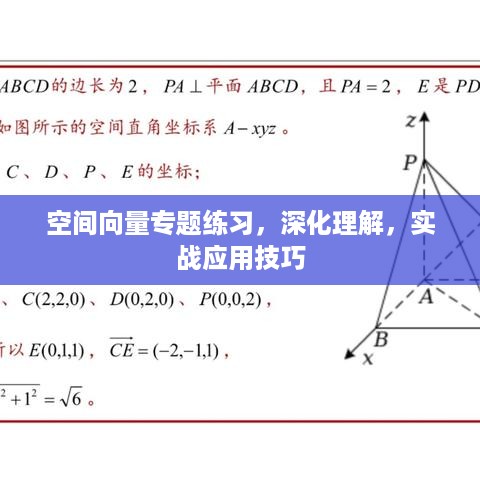
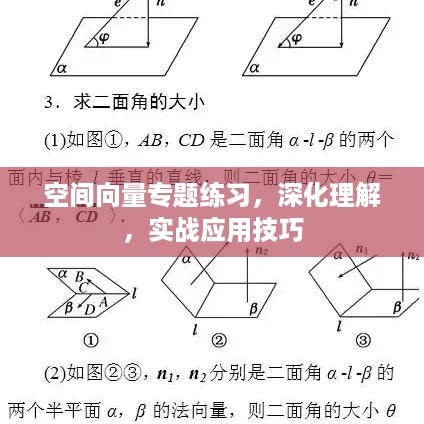
3、立体几何问题：利用空间向量解决立体几何中的距离、体积等问题。

4、物理学中的应用：理解空间向量在力学、运动学等领域的应用。

解题技巧与策略

1、熟练掌握空间向量的基本概念和性质，这是解题的基础。

2、学会运用向量运算法则解决实际问题，如力的合成与分解、平面几何和立体几何问题。

3、在解题过程中，要注意单位换算和计算精度，确保结果的准确性。

4、对于复杂问题，可以尝试建立坐标系，通过向量坐标进行计算。

通过本文的专题练习，读者应能够全面理解和掌握空间向量的相关知识，提高实战应用能力，空间向量在数学、物理等领域具有广泛的应用价值，掌握其基本概念、性质、运算及解题技巧，将有助于解决实际问题，建议读者在实际应用中不断练习，深化理解，提高技能。

练习题及答案

（此处可附加一系列练习题，包括选择题、填空题和解答题，以及对应的答案和解析。）

参考文献

（列举相关参考文献，以便读者进一步深入学习。）

附录

（提供一些有助于理解空间向量的相关资料，如图表、公式等。）

空间向量专题练习是深化理解和提高实战应用能力的重要途径，通过专题练习，读者应能够全面理解和掌握空间向量的相关知识，为解决实际问题打下坚实的基础。